3600
Câu 1: Trường hợp nào sau đây là công thức rút gọn của mạng:
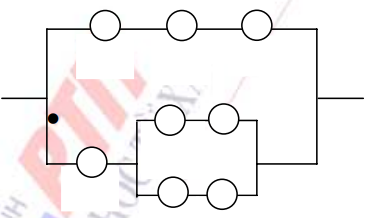
Correct!
Wrong!
Câu 2: Trường hợp nào sau đây tập R3 với các phép toán được định nghĩa là không gian véc tơ:
Correct!
Wrong!
Câu 3: Với các phép cộng hai hàm số và phép nhân hàm số với số thực, tập các hàm số nào sau đây là không gian véc tơ:
Correct!
Wrong!
Câu 4: Tập hợp các véc tơ có dạng nào sau đây không là không gian con của R3 :
Correct!
Wrong!
Câu 5: Tập hợp các véc tơ có dạng nào sau đây không là không gian con của R3 :
Correct!
Wrong!
Câu 6: Tìm véc tơ u sau của không gian R4 thỏa mãn phương trình:
Correct!
Wrong!
Câu 7: Hãy xác định
Correct!
Wrong!
Câu 8: Hệ véc tơ nào sau đây sinh ra R3:
Correct!
Wrong!
Câu 9: Hệ véc tơ nào sau đây của R3 thuộc độc lập tuyến tính:
Correct!
Wrong!
Câu 10: Hệ véc tơ nào dưới đây là độc lập tuyến tính?
Correct!
Wrong!
Câu 11: Tìm
Correct!
Wrong!
Câu 12: Xác định hệ véc tơ nào sau đây là một cơ sở của không gian R3:
Correct!
Wrong!
Câu 13: Xác định toạ độ của véc tơ
Correct!
Wrong!
Câu 14: Tìm chiều của các không gian con của R4:
Correct!
Wrong!
Câu 15: Tìm hạng r của hệ véc tơ sau của không gian R4:
Correct!
Wrong!
Câu 16: Phép toán nào sau đây không thực hiện được:
Correct!
Wrong!
Câu 17: Phép biến đổi nào sau đây không phải là phép biến đổi tương đương của hệ phương trình:
Correct!
Wrong!
Câu 18: Tìm các giá trị của tham số m để hệ phương trình sau có duy nhất nghiệm:
Correct!
Wrong!
Câu 19: Cho hệ phương trình tuyến tính:
Correct!
Wrong!
Câu 20: Giải hệ phương trình tuyến tính
Correct!
Wrong!
Thi thử trắc nghiệm ôn tập môn Toán cao cấp A2 online - Đề #3
Thi thử trắc nghiệm ôn tập môn Toán cao cấp A2 online – Đề #3 ngay tại ‘Toán cao cấp A2’ trên Tracnghiem123 để nhanh chóng và dễ dàng chuẩn bị cho kỳ thi. Đảm bảo giúp bạn tự tin hơn trong việc đạt kết quả cao.

