Đề thi thử THPT QG 2022 Toán online - Trường THPT Trí Đức

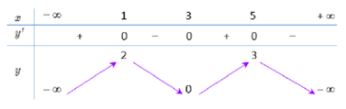
Câu 1: Cho hàm số y = f

x

có bảng biến thiên cho bởi bảng sau:Kết luận nào sau đây sai?

A. Giá trị cực tiểu của hàm số bằng 3.

B. f

x

đồng biến trên mỗi khoảng

(- \infty; 1), (3; 5)

.

C. Điểm cực đại của đồ thị hàm số là

1; 2

,

5; 3

.

D. f

x

nghịch biến trên môĩ khoảng

(1; 3), (5; + \infty)

.

Correct! Wrong!

Câu 2: Cho hàm số

y = \frac{3}{x - 2}

. Số tiệm cận của đồ thị hàm số bằng :

A. 0

B. 2

C. 3

D. 1

Correct! Wrong!

Câu 3: Cho hàm số

y = f (x) = x^{3} - 3 x^{2} - 4 x

. Diện tích hình phẳng giới hạn bởi đồ thị hàm số trên và trục Ox được tính bằng công thức:

A.

| \int_{- 1}^{4} f (x) d x |

.

B.

\int_{- 1}^{4} f (x) d x

.

C.

\int_{- 1}^{0} f (x) d x + \int_{0}^{4} f (x) d x

.

D.

\int_{- 1}^{0} f (x) d x - \int_{0}^{4} f (x) d x

.

Correct! Wrong!

Câu 4: Cho

I = \int_{1}^{2} 2 x \sqrt{x^{2} - 1} d x, u = x^{2} - 1

. Khẳng định nào dưới đây sai ?

A.

I = \int_{0}^{3} \sqrt{u} d u

.

B.

I = \frac{2}{3} \sqrt{27}

.

C.

\int_{1}^{2} \sqrt{u} d u

.

D.

I = \frac{2}{3} u^{\frac{3}{2}} | \begin{array}{l} 3 \\ 0 \end{array}

.

Correct! Wrong!

Câu 5: Hình nào sau đây có mặt phẳng đối xứng?

A. hình tứ diện

B. hình chóp có đáy là hình vuông

C. hình chóp tam giác đều

D. hình chóp có đáy là hình chữ nhật

Correct! Wrong!

Câu 6: Cho hình chóp

S . A B C D

có

A B C D

là hình vuông tại

A

và

D

thỏa mãn

S A ⊥ (A B C D)

và

A B = 2 A D = 2 C D = 2 a = \sqrt{2} S A

. Thể tích khối chóp

S . B C D

là:

A.

\frac{2 a^{3} \sqrt{2}}{3}

B.

\frac{a^{3} \sqrt{2}}{6}

C.

\frac{2 a^{3}}{3}

D.

\frac{a^{3} \sqrt{2}}{12}

Correct! Wrong!

Câu 7: Tỉ số thể tích của khối trụ nội tiếp và khối trụ ngoại tiếp hình lập phương có cạnh bằng

a

bằng

A.

\frac{1}{2} .

B.

\frac{1}{3} .

C.

\frac{1}{6} .

D.

\frac{1}{4} .

Correct! Wrong!

Câu 8: Mặt cầu tâm

I (2; 4; 6)

tiếp xúc với trục Oz có phương trình:

A.

{(x - 2)}^{2} + {(y - 4)}^{2} + {(z - 6)}^{2} = 20.

B.

{(x - 2)}^{2} + {(y - 4)}^{2} + {(z - 6)}^{2} = 40.

C.

{(x - 2)}^{2} + {(y - 4)}^{2} + {(z - 6)}^{2} = 52.

D.

{(x - 2)}^{2} + {(y - 4)}^{2} + {(z - 6)}^{2} = 56.

Correct! Wrong!

Câu 9: Với a, b là các số dương. Giá trị biểu thức

\frac{a^{\frac{1}{3}} \sqrt{b} + b^{\frac{1}{3}} \sqrt{a}}{\sqrt[6]{a} + \sqrt[6]{b}}

là:

A.

\sqrt[3]{a^{2} b^{2}}

B.

\sqrt[3]{a b}

C.

\sqrt{a^{3} b^{3}}

D. 1

Correct! Wrong!

Câu 10: Nghiệm của bất phương trình

(8, 5)^{\frac{x - 3}{x^{2} + 1}} < 1

là:

A.

(- \infty; 3]

B.

[3; + \infty)

C.

(- 3; 3)

D.

(- \infty; 3)

Correct! Wrong!

Câu 11: Tìm b, c

\in R

để phương trình

2 z^{2} - b z + c = 0

có hai nghiệm thuần ảo.

A.

{\begin{cases} b > 0 \\ c = 0 \end{cases}

.

B.

{\begin{cases} b = 0 \\ c < 2 \end{cases}

.

C.

{\begin{cases} b = 0 \\ c > - 2 \end{cases}

.

D.

{\begin{cases} b = 0 \\ c > 0 \end{cases}

.

Correct! Wrong!

Câu 12: Số phức

z = \frac{3 + 4 i}{2 + 3 i} + \frac{5 - 2 i}{2 - 3 i}

bằng:

A.

\frac{34}{13} + \frac{10}{13} i

.

B.

\frac{34}{13} - \frac{10}{13} i

.

C.

- \frac{34}{13} + \frac{10}{13} i

.

D.

- \frac{34}{13} - \frac{10}{13} i

.

Correct! Wrong!

Câu 13: Mặt cầu

(S)

có thể tích

36 π c m^{3}

. Diện tích của mặt cầu

(S)

bằng

A.

24 π c m^{2} .

B.

36 π c m^{2} .

C.

18 π c m^{2} .

D.

20 π c m^{2} .

Correct! Wrong!

Câu 14: Mặt cầu

(S)

có diện tích

16 π c m^{2}

. Diện tích của đường tròn lớn của mặt cầu

(S)

bằng

A.

4 π c m^{2} .

B.

6 π c m^{2} .

C.

8 π c m^{2} .

D.

2 π c m^{2} .

Correct! Wrong!

Câu 15: Cho mặt cầu

(S)

:

{(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 9

. Phương trình mặt cầu nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu

S

qua mặt phẳng

O x y

:

A.

{(x + 1)}^{2} + {(y + 2)}^{2} + {(z + 3)}^{2} = 9.

B.

{(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 9.

C.

{(x - 1)}^{2} + {(y + 2)}^{2} + {(z + 3)}^{2} = 9.

D.

{(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 9.

Correct! Wrong!

Câu 16: Cho mặt cầu

(S)

:

{(x + 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4

. Phương trình mặt cầu nào sau đây là phương trình mặt cầu đối xứng với mặt cầu

S

qua trục Oz:

A.

{(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4.

B.

{(x + 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4.

C.

{(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4.

D.

{(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 4.

Correct! Wrong!

Câu 17: Đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số

y = \frac{1 - 2 x}{- x + 2}

là:

A. x= - 2; y= - 2

B. x= 2; y = - 2

C. x = - 2; y= 2

D. x = 2; y = 2

Correct! Wrong!

Câu 18: Hàm số

y = x^{3} - 3 x^{2} + 3 x - 4

có bao nhiêu cực trị ?

A. 1

B. 2

C. 0

D. 3

Correct! Wrong!

Câu 19: Cho

c = \log_{15} 3

. Khi đó giá trị của

\log_{25} 15

theo c là:

A. 1 – c

B. 2c + 1

C.

\frac{1}{2 (1 - c)}

D.

\frac{1}{1 - c}

Correct! Wrong!

Câu 20: Tìm khẳng định sai trong các khẳng định sau:

A.

\int_{a}^{b} [f (x) + g (x)] d x = \int_{a}^{b} f (x) d x + \int_{a}^{b} g (x) d x

.

B. f

x

liên tục trên

a; c

và a < b < c thì

\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{b}^{c} f (x) d x

.

C. Nếu

f (x) \geq 0

trên đoạn

a; b

thì

\int_{a}^{b} f (x) d x \geq 0

.

D.

\int \frac{u^{'} (x) d x}{u (x)} = \ln | u (x) | + C

.

Correct! Wrong!

Câu 21: Cho hai nghiệm

z_{1} = - \sqrt{3} + i \sqrt{2}, z_{2} = - \sqrt{3} - i \sqrt{2}

. Phương trình bậc hai có nghiệm là hai nghiệm trên là:

A.

z^{2} + 3 \sqrt{2} z + 5 = 0

.

B.

z^{2} + 2 \sqrt{3} z + 5 = 0

.

C.

z^{2} - 2 \sqrt{3} z + 5 = 0

.

D.

z^{2} + 5 z + 2 \sqrt{3 = 0}

.

Correct! Wrong!

Câu 22: Số mặt phẳng đối xứng của mặt cầu là:

A.

6

B.

3

C.

0

D. Vô số

Correct! Wrong!

Câu 23: Cho măt cầu

(S)

tâm

O

, có bán kính bằng

r = 5 c m

. Đường thẳng

Δ

cắt mặt cầu

(S)

theo một dây cung

A B = 6 c m

. Khoảng cách từ

O

đến đường thẳng

Δ

bằng

A.

3 c m .

B.

4 \sqrt{2} c m

.

C.

5 c m .

D.

4 c m .

Correct! Wrong!

Câu 24: Đường tròn giao tuyến của

(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 16

khi cắt bởi mặt phẳng

O x y

có chu vi bằng:

A.

\sqrt{7} π .

B.

2 \sqrt{7} π .

C.

7 π .

D.

14 π .

Correct! Wrong!

Câu 25: Tìm nguyên hàm của hàm số

f (x) = e^{x} (1 - 3 e^{- 2 x})

.

A.

F (x) = e^{x} - 3 e^{- 3 x} + C

.

B.

F (x) = e^{x} + 3 e^{- x} + C

.

C.

F (x) = e^{x} - 3 e^{- x} + C

.

D.

F (x) = e^{x} + C

.

Correct! Wrong!

Câu 26: Cho

\int_{1}^{4} f (x) d x = 9

. Tính tích phân

I = \int_{0}^{1} f (3 x + 1) d x

.

A. I= 27

B. I= 3

C. I= 9

D. I= 1

Correct! Wrong!

Câu 27: Cho f

x

, g

x

là hai hàm số liên tục trên R và

k \neq 0

. Chọn khẳng định sai trong các khẳng định sau đây .

A.

\int [f (x) . g (x)] d x = \int f (x) d x . \int g (x) d x

B.

\int k . f (x) d x = k \int f (x) d x

C.

\int f^{'} (x) d x = f (x) + C

D.

\int [f (x) \pm g (x)] d x = \int f (x) d x \pm \int g (x) d x

Correct! Wrong!

Câu 28: Cho số thực a thỏa mãn

\int_{- 1}^{a} e^{x + 1} d x = e^{2} - 1

. Khi đó a có giá trị bằng:

A. 0

B. -1

C. 1

D. 2

Correct! Wrong!

Câu 29: Giá trị cực đại của hàm số

y = x^{3} - 12 x - 1

.

A. – 17

B. – 2

C. 45

D. 15

Correct! Wrong!

Câu 30: Đồ thi hàm số nào dưới đây có tiệm cận đứng

A.

y = x

B.

y = x^{3} - 2 x^{2} + 1

C.

y = \frac{2 x}{x - 1}

D.

y = \frac{π}{x^{2} - x + 1}

Correct! Wrong!

Câu 31:

A. a + b

B. a + b + 1

C. 2a + 2b – 2

D. a + b – 1

Correct! Wrong!

Câu 32: Với 0 < a < b,

m \in N^{*}

thì:

A.

a^{m} < b^{m}

B.

a^{m} > b^{m}

C.

1 < a^{m} < b^{m}

D.

a^{m} > b^{m} > 1

Correct! Wrong!

Câu 33: Cho số phức thỏa mãn điều kiện

| z - 2 + 2 i | = 1

. Tìm giá trị lớn nhất của

| z |

.

A.

max | z | = 2 \sqrt{2} + 1

.

B.

max | z | = 2 \sqrt{2}

.

C.

max | z | = 2 \sqrt{2} + 2

.

D.

max | z | = 2 \sqrt{2} - 1

.

Correct! Wrong!

Câu 34: Phần thực và phần ảo của số phức

z = {(1 + \sqrt{3} i)}^{2}

là:

A. 1 và 3.

B. 1 và – 3.

C. – 2 và

2 \sqrt{3}

.

D. 2 và

- 2 \sqrt{3}

.

Correct! Wrong!

Câu 35: Có tất cả bao nhiêu khối đa diện đều?

A.

5

B.

4

C. Vô số

D.

3

Correct! Wrong!

Câu 36: Mặt cầu tiếp xúc với các cạnh của tứ diện đều

A B C D

cạnh

a

có bán kính là?

A.

\frac{a \sqrt{2}}{2} .

B.

\frac{a \sqrt{2}}{4} .

C.

a \sqrt{2} .

D.

2 a \sqrt{2} .

Correct! Wrong!

Câu 37: Trong không gian với hệ toạ độ

O x y z

,tọa độ điểm

M

nằm trên trục

O y

và cách đều hai mặt phẳng:

(P) : x + y - z + 1 = 0

và

(Q) : x - y + z - 5 = 0

là:

A.

M (0; - 3; 0)

.

B.

M (0; 3; 0)

.

C.

M (0; - 2; 0)

.

D.

M (0; 1; 0)

.

Correct! Wrong!

Câu 38: Chọn khẳng định đúng trong các khẳng định sau:

A. Hình bát diện đều có 8 đỉnh

B. Hình bát diện đều có các mặt là bát giác đều

C. Hình bát diện dều có các mặt là hình vuông

D. Hình bát diện đều là đa diện đều loại {3;4}

Correct! Wrong!

Câu 39: Cho hàm số

y = \frac{x + 1}{x - 1}

. Khẳng định nào sau đây là đúng ?

A. Hàm số đã cho nghịch biến trên khoảng

(- \infty; 1)

.

B. Hàm số đã cho đồng biến trên khoảng

(- \infty; 1), (1; + \infty)

.

C. Hàm số đã cho đồng biến trên khoảng

(0; + \infty)

.

D. Hàm số đã cho nghịch biến trên tập R.

Correct! Wrong!

Câu 40: Cho hàm số y = f

x

xác định trên khoảng

(0; + \infty)

và thỏa mãn

lim_{x \to + \infty} f (x) = 1

. Hãy chọn mệnh đề đúng trong các mệnh đề sau:

A. Đường thẳng x = 1 là tiệm cận ngang của đồ thị hàm số y = f

x

.

B. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số y = f

x

.

C. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số y = f

x

.

D. Đường thẳng y = 1 là tiệm cận đứng của đồ thị hàm số y = f

x

.

Correct! Wrong!

Câu 41: Tích phân

I = \int_{\frac{π}{3}}^{\frac{π}{2}} \frac{d x}{\sin x}

có giá trị bằng:

A.

2 \ln \frac{1}{3}

.

B.

2 \ln 3

.

C.

\frac{1}{2} \ln 3

.

D.

\frac{1}{2} \ln \frac{1}{3}

.

Correct! Wrong!

Câu 42: Tích phân

I = \int_{1}^{e} 2 x (1 - \ln x) d x

bằng :

A.

\frac{e^{2} - 1}{2}

.

B.

\frac{e^{2} + 1}{2}

.

C.

\frac{e^{2} - 3}{4}

.

D.

\frac{e^{2} - 3}{2}

.

Correct! Wrong!

Câu 43: Cho khối hộp ABCD. A’B’C’D’. Gọi O là giaocủa AC và BD. Tính tỷ số thể tích của khối chóp O. A’B’C’D’ và khối chóp đã cho.

A.

\frac{1}{3}

B.

\frac{1}{6}

C.

\frac{1}{2}

D.

\frac{1}{4}

Correct! Wrong!

Câu 44: Trong không gian với hệ toạ độ

O x y z

, gọi

(α)

là mặt phẳng song song với mặt phẳng

(β) : 2 x - 4 y + 4 z + 3 = 0

và cách điểm

A (2; - 3; 4)

một khoảng

k = 3

. Phương trình của mặt phẳng

(α)

là:

A.

2 x - 4 y + 4 z - 5 = 0

hoặc

2 x - 4 y + 4 z - 13 = 0

.

B.

x - 2 y + 2 z - 25 = 0

.

C.

x - 2 y + 2 z - 7 = 0

.

D.

x - 2 y + 2 z - 25 = 0

hoặc

x - 2 y + 2 z - 7 = 0

.

Correct! Wrong!

Câu 45: Nếu n chẵn thì điều kiện để

\sqrt[n]{b}

có nghĩa là:

A. b < 0

B.

b \leq 0

C. b > 0

D.

b \geq 0

Correct! Wrong!

Câu 46: Chọn mệnh đề đúng:

A.

2^{\log_{2} 3} = 5^{\log_{3} 5}

B.

2^{\log_{2} 3} = 5^{\log_{5} 3}

C.

5^{\log_{5} 3} = \log_{2} 3

D.

2^{\log_{2} 4} = 2

Correct! Wrong!

Câu 47: Cho số phức z có điểm biểu diễn nằm trên đường thẳng 3x – 4y – 3 =0,

| z |

nhỏ nhất bằng:

A.

\frac{1}{5}

B.

\frac{4}{5}

C.

\frac{2}{5}

D.

\frac{3}{5}

.

Correct! Wrong!

Câu 48: Mô đun của số phức z thỏa mãn

\overset{―}{z} = 8 - 6 i

là:

A. 2

B. 10

C. 14

D.

2 \sqrt{7}

Correct! Wrong!

Câu 49: Trong không gian với hệ toạ độ

O x y z

,cho hai đường thẳng

d_{1}, d_{2}

lần lượt có phương trình

d_{1} : \frac{x - 2}{2} = \frac{y - 2}{1} = \frac{z - 3}{3}

,

d_{2} : \frac{x - 1}{2} = \frac{y - 2}{- 1} = \frac{z - 1}{4}

. Phương trình mặt phẳng

(α)

cách đều hai đường thẳng

d_{1}, d_{2}

là:

A.

7 x - 2 y - 4 z = 0

.

B.

7 x - 2 y - 4 z + 3 = 0

.

C.

2 x + y + 3 z + 3 = 0

.

D.

14 x - 4 y - 8 z + 3 = 0

.

Correct! Wrong!

Câu 50: Trong không gian

{(x + 4)}^{2} + {(y + 1)}^{2} + {(z + 6)}^{2} = 18.

, cho mặt phẳng

{(x - 4)}^{2} + {(y - 1)}^{2} + {(z - 6)}^{2} = 9.

:

{(x - 4)}^{2} + {(y - 1)}^{2} + {(z - 6)}^{2} = 16.

và đường thẳng

d

:

N (- 5; 7; 0)

. Với giá trị nào của

\vec{u} = (2; - 2; 1)

thì

\vec{M N} = (- 9; 6; - 6)

cắt

H

A.

(S)

.

B.

(S)

.

C.

R^{2} = M H^{2} + {(\frac{A B}{2})}^{2} = 18

.

D.

d (M, d) = 3

.

Correct! Wrong!

Đề thi thử THPT QG năm 2022 môn Toán online – Đề thi của Trường THPT Trí Đức

Thi thử tốt nghiêp THPT quốc gia môn Toán – Đề thi chính thức năm 2022 của Bộ GD&ĐT

Đề thi thử THPT QG năm 2022 môn Toán online – Đề thi của Trường THPT Lương Thế Vinh

Đề thi thử THPT QG năm 2022 môn Toán online – Đề thi của Trường THPT Nguyễn Du

LEAVE A REPLY Cancel reply

Most Popular

Thi thử tốt nghiêp THPT quốc gia môn Toán – Đề thi chính thức năm 2022 của Bộ GD&ĐT

Thi thử trắc nghiệm ôn tập Chi tiết máy online – Đề #9

Đề thi thử học kỳ 1 môn Hoá Học lớp 11 online – Mã đề 17

Thi thử trắc nghiệm môn Lý thuyết điều khiển tự động online – Đề #1

Recent Comments

EDITOR PICKS

Thi thử tốt nghiêp THPT quốc gia môn Toán – Đề thi chính thức năm 2022 của Bộ GD&ĐT

Thi thử trắc nghiệm ôn tập Chi tiết máy online – Đề #9

Đề thi thử học kỳ 1 môn Hoá Học lớp 11 online – Mã đề 17

POPULAR POSTS

Thi thử tốt nghiêp THPT quốc gia môn Toán – Đề thi chính thức năm 2022 của Bộ GD&ĐT

Thi thử trắc nghiệm ôn tập Chi tiết máy online – Đề #9

Đề thi thử học kỳ 1 môn Hoá Học lớp 11 online – Mã đề 17

POPULAR CATEGORY

ABOUT US

FOLLOW US