5400
Câu 1: Hàm số nào dưới đây đồng biến trên khoảng
Correct!
Wrong!
Câu 2: Cho khối lăng trụ
Correct!
Wrong!
Câu 3: Cho đồ thị hàm số như hình vẽ. Mệnh đề nào dưới đây là đúng ?
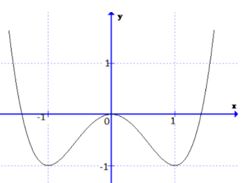
Correct!
Wrong!
Câu 4: Phép tịnh tiến biến gốc tọa độ
Correct!
Wrong!
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng ?- Nếu
Correct!
Wrong!
Câu 6: Tìm tập nghiệm
Correct!
Wrong!
Câu 7: Tìm tập xác định
Correct!
Wrong!
Câu 8: Cho hàm số
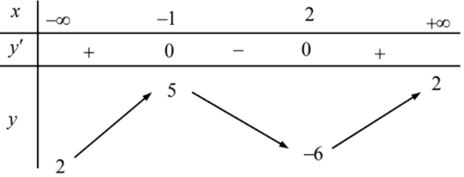
Correct!
Wrong!
Câu 9: Tìm nguyên hàm của hàm số
Correct!
Wrong!
Câu 10: Cho hình chóp
Correct!
Wrong!
Câu 11: Trong không gian với hệ tọa độ
Correct!
Wrong!
Câu 12: Trong các mệnh đề sau, mệnh đề nào đúng? Số các cạnh của hình đa diện luôn luôn …
Correct!
Wrong!
Câu 13: Cho
Correct!
Wrong!
Câu 14: Phương trình
Correct!
Wrong!
Câu 15: Trong không gian với hệ tọa độ
Correct!
Wrong!
Câu 16: Rút gọn biểu thức
Correct!
Wrong!
Câu 17: Trong không gian với hệ tọa độ
Correct!
Wrong!
Câu 18: Cho
Correct!
Wrong!
Câu 19: Trong không gian với hệ tọa độ
Correct!
Wrong!
Câu 20: Cho hàm số
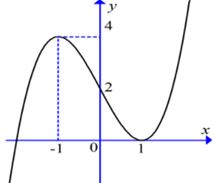
Correct!
Wrong!
Câu 21: Biết hệ số của
Correct!
Wrong!
Câu 22: Bình có bốn đôi giày khác nhau gồm bốn màu: đen, trắng, xanh và đỏ. Một buổi sáng đi học, vì vội vàng, Bình đã lấy ngẫu nhiên hai chiếc giày từ bốn đôi giày đó. Tính xác suất để Bình lấy được hai chiếc giày cùng màu.
Correct!
Wrong!
Câu 23: Cho phương trình lượng giác
Correct!
Wrong!
Câu 24: Sinh nhật bạn của An vào ngày 01 tháng năm. An muốn mua một món quà sinh nhật cho bạn nên quyết định bỏ ống heo 100 đồng vào ngày 01 tháng 01 năm 2016, sau đó cứ liên tục ngày sau hơn ngày trước 100 đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền ?
Correct!
Wrong!
Câu 25: Nếu
Correct!
Wrong!
Câu 26: Tìm giá trị thực của tham số
Correct!
Wrong!
Câu 27: Khi quay một tam giác đều cạnh bằng
Correct!
Wrong!
Câu 28: Cho
Correct!
Wrong!
Câu 29: Cho
Correct!
Wrong!
Câu 30: Tìm giá trị thực của tham số
Correct!
Wrong!
Câu 31: Tìm tập nghiệm
Correct!
Wrong!
Câu 32: Cho hàm số
Correct!
Wrong!
Câu 33: Cho hình chóp
Correct!
Wrong!
Câu 34: Cho hàm số
Correct!
Wrong!
Câu 35: Để đóng học phí học đại học, bạn An vay ngân hàng số tiền 9.000.000 đồng, lãi suất 3%/năm trong thời hạn 4 năm với thể thức cứ sau mỗi năm, số tiền lãi sẽ được nhập vào nợ gốc để tính lãi cho năm tiếp theo. Sau bốn năm, đến thời hạn trả nợ, hai bên thỏa thuận hình thức trả nợ như sau: lãi suất cho vay được điều chỉnh thành 0,25%/tháng, đồng thời hàng tháng bạn An phải trả nợ cho ngân hàng số tiền T không đổi và cứ sau mỗi tháng, số tiền T sẽ được trừ vào tiền nợ gốc để tính lãi cho tháng tiếp theo. Hỏi muốn trả hết nợ ngân hàng trong 5 năm thì hàng tháng bạn An phải trả cho ngân hàng số tiền T là bao nhiêu ?
Correct!
Wrong!
Câu 36: Tìm
Correct!
Wrong!
Câu 37: Cho hàm số
Correct!
Wrong!
Câu 38: Gọi
Correct!
Wrong!
Câu 39: Có 10 đội bóng thi đấu theo thể thức vòng tròn một lượt, thắng được 3 điểm, hòa 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng cộng điểm số của tất cả 10 đội là 130. Hỏi có bao nhiêu trận hòa ?
Correct!
Wrong!
Câu 40: Cho hình trụ
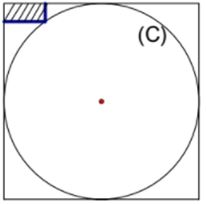
Correct!
Wrong!
Câu 41: Cho hình chóp
Correct!
Wrong!
Câu 42: Cho hàm số
Correct!
Wrong!
Câu 43: Cho hình lăng trụ đứng
Correct!
Wrong!
Câu 44: Cho hàm số
Correct!
Wrong!
Câu 45: Tính giá trị của biểu thức
Correct!
Wrong!
Câu 46: Xét các số thực
Correct!
Wrong!
Câu 47: Cho
Correct!
Wrong!
Câu 48: Cho hàm số
Correct!
Wrong!
Câu 49: Cho dãy số
Correct!
Wrong!
Câu 50: Tìm giá trị lớn nhất của hàm số sau
Correct!
Wrong!
Đề thi thử THPT QG năm 2022 môn Toán online - Đề thi của Trường THPT Ngô Quyền
Muốn chuẩn bị tốt cho kỳ thi THPT Quốc Gia năm 2022, học sinh cần ôn tập và làm đề thi thử. Tracnghiem123 cung cấp đề thi thử môn Toán của Trường THPT Ngô Quyền online, giúp học sinh dễ dàng và nhanh chóng kiểm tra kiến thức. Hãy truy cập vào chuyên mục ‘Toán’ trên Tracnghiem123 để chuẩn bị tốt cho kỳ thi sắp tới.

