5400
Câu 1: Số cách chọn 5 học sinh trong 10 học sinh của một lớp đi tham quan di tích Ngã Ba Đồng Lộc là
Correct!
Wrong!
Câu 2: Cho một cấp số cộng
Correct!
Wrong!
Câu 3: Cho hàm số
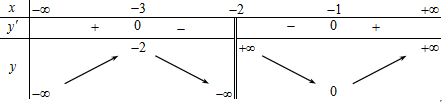
Correct!
Wrong!
Câu 4: Cho hàm số
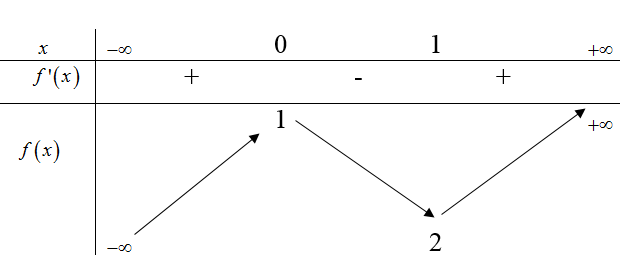
Correct!
Wrong!
Câu 5: Cho hàm số
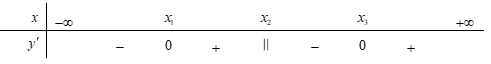
Correct!
Wrong!
Câu 6: Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
Correct!
Wrong!
Câu 7: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
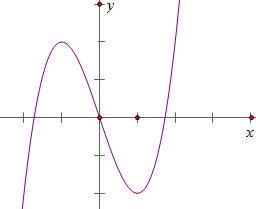
Correct!
Wrong!
Câu 8: Số giao điểm của đồ thị hàm số
Correct!
Wrong!
Câu 9: Với a là số thực dương tùy ý,
Correct!
Wrong!
Câu 10: Đẳng thức nào sau đây đúng với mọi số dương
Correct!
Wrong!
Câu 11: Rút gọn biểu thức
Correct!
Wrong!
Câu 12: Phương trình
Correct!
Wrong!
Câu 13: Tổng bình phương các nghiệm của phương trình
Correct!
Wrong!
Câu 14: Tìm các nguyên hàm của hàm số
Correct!
Wrong!
Câu 15: Nguyên hàm của hàm số
Correct!
Wrong!
Câu 16: Cho
Correct!
Wrong!
Câu 17: Tính tích phân
Correct!
Wrong!
Câu 18: Số phức liên hợp của số phức z = 2020 - 2021i
Correct!
Wrong!
Câu 19: Cho hai số phức
Correct!
Wrong!
Câu 20: Cho số phức z=4-5i. Trên mặt phẳng tọa độ, điểm biểu diễn của số phức
Correct!
Wrong!
Câu 21: Một khối lăng trụ có chiều cao bằng 2a và diện tích đáy bằng
Correct!
Wrong!
Câu 22: Cho khối chóp có diện tích đáy bằng
Correct!
Wrong!
Câu 23: Gọi
Correct!
Wrong!
Câu 24: Tính theo
Correct!
Wrong!
Câu 25: Trong không gian Oxyz, cho hai điểm
Correct!
Wrong!
Câu 26: Trong không gian với hệ tọa độ Oxyz, tọa độ tâm I và bán kính
Correct!
Wrong!
Câu 27: Trong không gian Oxyz, điểm nào dưới đây nằm trên mặt phẳng
Correct!
Wrong!
Câu 28: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
Correct!
Wrong!
Câu 29: Gieo một con súc sắc ba lần. Xác suất để được mặt số hai xuất hiện cả ba lần là.
Correct!
Wrong!
Câu 30: Tìm các khoảng đồng biến của hàm số
Correct!
Wrong!
Câu 31: Cho hàm số
Correct!
Wrong!
Câu 32: Tập nghiệm của bất phương trình
Correct!
Wrong!
Câu 33: Cho
Correct!
Wrong!
Câu 34: Cho hai số phức
Correct!
Wrong!
Câu 35: Cho hình chóp S.ABC có SA=SB=CB=CA, hình chiếu vuông góc của S lên mặt phẳng
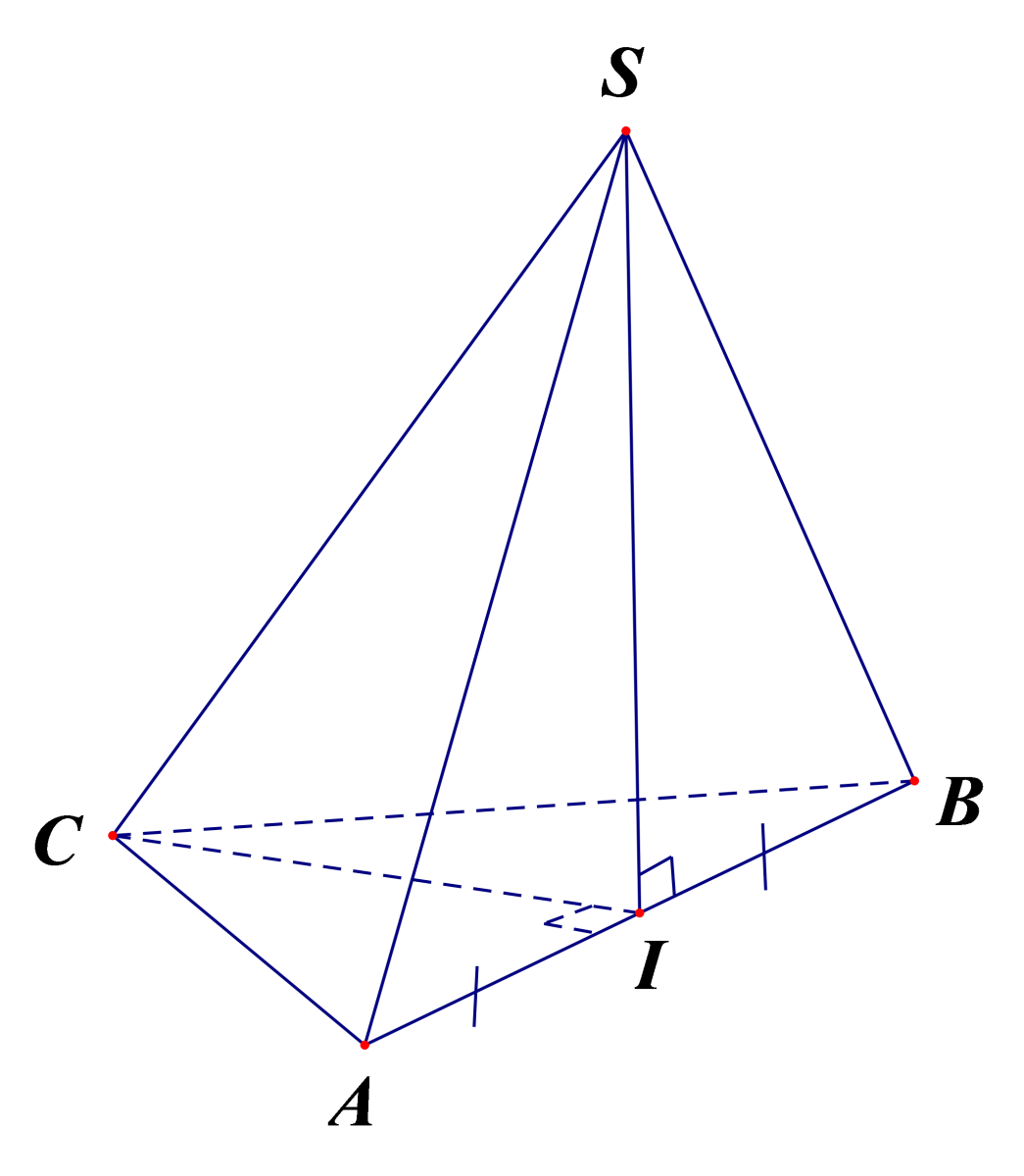
Correct!
Wrong!
Câu 36: Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a. Gọi M là trung điểm của SD. Khoảng cách từ M đến mặt phẳng
Correct!
Wrong!
Câu 37: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu
Correct!
Wrong!
Câu 38: Trong không gian với hệ tọa độ Oxyz, viết phương trình tham số của đường thẳng
Correct!
Wrong!
Câu 39: Cho đồ thị hàm số y = f

Correct!
Wrong!
Câu 40: Tìm tất cả các giá trị của tham số m để bất phương trình sau
Correct!
Wrong!
Câu 41: Cho
Correct!
Wrong!
Câu 42: Cho số phức
Correct!
Wrong!
Câu 43: Cho hình chóp S.ABC có mặt phẳng
Correct!
Wrong!
Câu 44: Cổng trường Đại học Bách Khoa Hà Nội có hình dạng Parabol, chiều rộng
Correct!
Wrong!
Câu 45: Trong không gian Oxyz, cho đường thẳng
Correct!
Wrong!
Câu 46: Hình vẽ dưới đây là đồ thị của hàm số
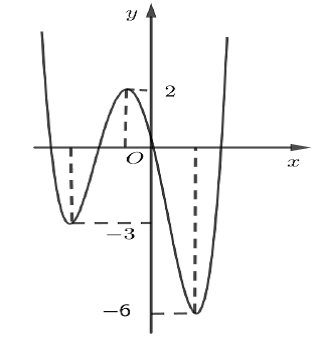
Correct!
Wrong!
Câu 47: Có bao nhiêu giá trị nguyên của tham số
Correct!
Wrong!
Câu 48: Gọi
Correct!
Wrong!
Câu 49: Cho số phức z và w thỏa mãn z+w=3+4i và
Correct!
Wrong!
Câu 50: Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
Correct!
Wrong!
Đề thi thử THPT QG năm 2021 môn Toán online - Đề thi của Trường THPT Trần Phú lần 2
Làm Đề thi thử THPT QG năm 2021 môn Toán online dễ dàng và nhanh chóng tại Tracnghiem123. Với đề thi của Trường THPT Trần Phú lần 2, bạn sẽ có cơ hội ôn tập và kiểm tra kiến thức một cách hiệu quả. Hãy truy cập ngay vào chuyên mục ‘Toán’ trên Tracnghiem123 để bắt đầu chuẩn bị cho kỳ thi quan trọng của mình.

